Bedenk wat voor variabelen je gaat gebruiken. Een schaakbord bestaat uit 64 vierkanten. In hoofdstuk 4 heb je geleerd dat je een (gevulde) rechthoek (en dus ook een vierkant) tekent met de opdrachten:
g.drawRect(x, y, breedte, hoogte); g.setColor(Color.BLACK); g.fillRect(x, y, breedte, hoogte);
Een schaakbord bestaat uit 8 x 8 = 64 velden. Je zou dus 64 keer een vierkant kunnen tekenen, maar dat betekent dat je enorm veel code moet schrijven. Door gebruik te maken van lussen gaan we proberen een stuk efficiënter te werken.
Een schaakbord kun je zien als een verzameling rijen en kolommen. In Java (en andere programmeertalen) is het gebruikelijk om te beginnen te tellen bij 0.
| rij 0 kolom 0 | rij 0 kolom 1 | rij 0 kolom 2 | rij 0 kolom 3 | rij 0 kolom 4 | rij 0 kolom 5 | rij 0 kolom 6 | rij 0 kolom 7 |
| rij 1 kolom 0 | rij 1 kolom 1 | rij 1 kolom 2 | rij 1 kolom 3 | rij 1 kolom 4 | rij 1 kolom 5 | rij 1 kolom 6 | rij 1 kolom 7 |
| rij 2 kolom 0 | rij 2 kolom 1 | rij 2 kolom 2 | rij 2 kolom 3 | rij 2 kolom 4 | rij 2 kolom 5 | rij 2 kolom 6 | rij 2 kolom 7 |
| rij 3 kolom 0 | rij 3 kolom 1 | rij 3 kolom 2 | rij 3 kolom 3 | rij 3 kolom 4 | rij 3 kolom 5 | rij 3 kolom 6 | rij 3 kolom 7 |
| rij 4 kolom 0 | rij 4 kolom 1 | rij 4 kolom 2 | rij 4 kolom 3 | rij 4 kolom 4 | rij 4 kolom 5 | rij 4 kolom 6 | rij 4 kolom 7 |
| rij 5 kolom 0 | rij 5 kolom 1 | rij 5 kolom 2 | rij 5 kolom 3 | rij 5 kolom 4 | rij 5 kolom 5 | rij 5 kolom 6 | rij 5 kolom 7 |
| rij 6 kolom 0 | rij 6 kolom 1 | rij 6 kolom 2 | rij 6 kolom 3 | rij 6 kolom 4 | rij 6 kolom 5 | rij 6 kolom 6 | rij 6 kolom 7 |
| rij 7 kolom 0 | rij 7 kolom 1 | rij 7 kolom 2 | rij 7 kolom 3 | rij 7 kolom 4 | rij 7 kolom 5 | rij 7 kolom 6 | rij 7 kolom 7 |
Begin met het tekenen van een rij vierkanten met behulp van een lus.
Dit kun je doen met behulp van de volgende for-lus:
public void paint(Graphics g) {
//de x en y coordinaten
int x = 50;
int y = 50;
for (int kolom = 0; kolom < 8; kolom++) {
g.drawRect(x, y, breedte, hoogte);
x += breedte;
}
}
Bij het tekenen van één rij velden van een schaakbord moeten we er voor zorgen dat de x-coördinaat bij ieder nieuw veld net zoveel naar rechts schuift als de breedte van het veld. Anders zouden de velden elkaar overlappen.
Nu gaan we er voor zorgen dat de velden om en om zwart en wit worden. Er zijn 8 velden (kolommen) genummerd 0 t/m 7. Het eerste veld moet zwart worden. Dit betekent dat als (if) kolom nummer 0, 2, 4 of 6 heeft, het veld zwart moet worden en anders (else) wit. Dit kun je uiteraard met een if-else-statement bewerkstelligen. Zie hoofdstuk 10.
public void paint(Graphics g) {
y = 50;
x = 50;
for (int kolom = 0; kolom < 8; kolom++) {
if (kolom == 0 || kolom == 2 || kolom == 4 || kolom == 6) {
g.setColor(zwart);
g.fillRect(x, y, breedte, hoogte);
} else {
g.setColor(wit);
g.fillRect(x, y, breedte, hoogte);
}
x += breedte;
}
}
Laten we nu een tweede rij maken. We moeten dan de Y-coördinaat met de hoogte van de cel verhogen om hem netjes onder de eerste rij te krijgen. Ook moeten we de kleuren omdraaien.
public void paint(Graphics g) {
y = 50;
x = 50;
for (int kolom = 0; kolom < 8; kolom++) {
if (kolom == 0 || kolom == 2 || kolom == 4 || kolom == 6) {
g.setColor(zwart);
g.fillRect(x, y, breedte, hoogte);
} else {
g.setColor(wit);
g.fillRect(x, y, breedte, hoogte);
}
x += breedte;
}
//tweede rij
x = 50;
y += hoogte;
for (int kolom = 0; kolom < 8; kolom++) {
if (kolom == 0 || kolom == 2 || kolom == 4 || kolom == 6) {
g.setColor(wit);
g.fillRect(x, y, breedte, hoogte);
} else {
g.setColor(zwart);
g.fillRect(x, y, breedte, hoogte);
}
x += breedte;
}
}
We moeten de X-coördinaat weer terug zetten naar zijn oorspronkelijke positie, anders krijgen we het volgende resultaat:

Als een waarde aan een variabele wordt toegekend, dan wordt die waarde onthouden tot de sluitaccolade van de body waarbinnen hij is gedeclareerd. Dit kan verwarrend zijn, met name als je gebruik maakt van lussen!
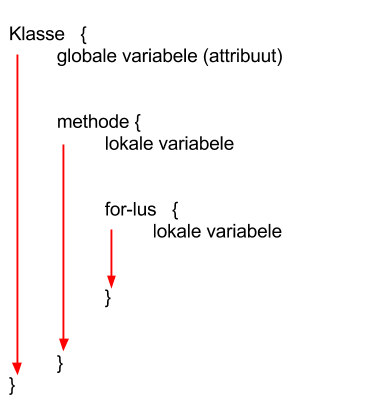
Bovenstaande code kun je herhalen tot het schaakbord compleet is. Maar het kan uiteraard nog veel korter door ook bij het maken van de 8 rijen gebruik te maken van een lus. Ga als volgt te werk:
Als het goed is gegaan beslaat je code nu nog maar zo'n 40 regels. Kun je manieren bedenken om het nog efficiënter te maken? Tip: kijk goed naar de tabel eerder op deze pagina om patronen te ontdekken die je kunt gebruiken in je algoritme.